ዝርዝር ሁኔታ:

ቪዲዮ: መስመራዊ ባልሆነ መረጃ ላይ ሪግሬሽን ማድረግ እንችላለን?
2024 ደራሲ ደራሲ: Miles Stephen | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-15 23:33
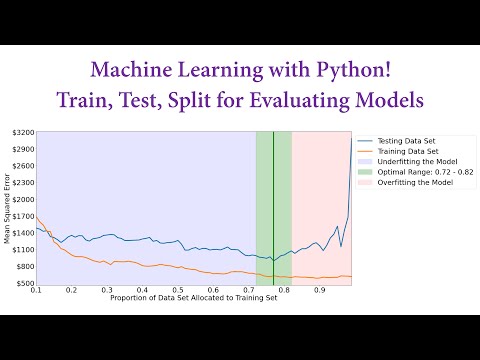
መስመር-አልባ ዳግም መመለስ ይችላል። ብዙ ተጨማሪ ዓይነት ኩርባዎችን ይስማማል ፣ ግን እሱ ይችላል በጣም ጥሩውን ለማግኘት እና ለመፈለግ የበለጠ ጥረት ይፈልጋሉ መተርጎም ገለልተኛ ተለዋዋጮች ሚና. በተጨማሪም፣ R-squared ለ አይሰራም ቀጥተኛ ያልሆነ መመለሻ , እና የማይቻል ነው አስላ p-values ለቅርብ ግምቶች.
በዚህ መንገድ፣ ሪግሬሽን መደበኛ ያልሆነ ሊሆን ይችላል?
በስታቲስቲክስ ፣ ቀጥተኛ ያልሆነ መመለሻ መልክ ነው። መመለሻ የትኛዎቹ ምልከታ መረጃ በተቀረጸው ተግባር ሀ መደበኛ ያልሆነ የአምሳያው መለኪያዎች ጥምረት እና በአንድ ወይም በብዙ ገለልተኛ ተለዋዋጮች ላይ የተመሠረተ ነው። ውሂቡ በተከታታይ ግምቶች ዘዴ የተገጠመ ነው።
እንዲሁም አንድ ሰው ሊጠይቅ ይችላል፣ r ስኩዌር የሆነው ለመስመራዊ መመለሻ ብቻ ነው? አጠቃላይ የሂሳብ ማዕቀፍ ለ አር - አራት ማዕዘን ከሆነ በትክክል አይሰራም የመመለሻ ሞዴል አይደለም መስመራዊ . ምንም እንኳን ይህ ችግር ቢኖርም, አብዛኛው የስታቲስቲክስ ሶፍትዌር አሁንም ይሰላል አር - አራት ማዕዘን ላልሆኑ ሞዴሎች. ከተጠቀሙ አር - አራት ማዕዘን ምርጡን ለመምረጥ ሞዴል , ወደ ተገቢው ይመራል ሞዴል ብቻ 28-43% ጊዜ.
ይህንን በተመለከተ፣ ቀጥተኛ ያልሆነ ሪግሬሽን እንዴት ማስላት ይቻላል?
የእርስዎ ሞዴል አንድ የሚጠቀም ከሆነ እኩልታ በ Y = a ቅጽ0 + ለ1X1፣ ሀ ነው። መስመራዊ ሪግሬሽን ሞዴል. ካልሆነ ግን ነው። መደበኛ ያልሆነ.
Y = f (X, β) + ε
- X = የ p ትንበያዎች ቬክተር ፣
- β = የ k መለኪያዎች ቬክተር ፣
- ረ (-) = የታወቀ የመልሶ ማቋቋም ተግባር ፣
- ε = የስህተት ቃል
የመልሶ ማቋቋም ዓይነቶች ምንድ ናቸው?
የመልሶ ማቋቋም ዓይነቶች
- መስመራዊ ሪግሬሽን. በጣም ቀላሉ የመልሶ ማቋቋም ዘዴ ነው.
- ፖሊኖሚል ሪግሬሽን. የገለልተኛ ተለዋዋጭ ፖሊኖሚል ተግባራትን በመውሰድ የመስመር ላይ ያልሆነ እኩልታ ለማስማማት ቴክኒክ ነው።
- የሎጂስቲክ ሪግሬሽን.
- Quantile Regression.
- ሪጅ ሪግሬሽን.
- Lasso Regression.
- የላስቲክ ኔት ሪግሬሽን.
- ዋና አካላት መመለሻ (PCR)
የሚመከር:
ፎሊየድ ባልሆነ እና በተቀረጸው ሜታሞርፊክ ዓለት መካከል ያለው ልዩነት ምንድን ነው?

እንደ gneiss፣ phyllite፣ schist እና slate ያሉ ፎላይድ ሜታሞርፊክ አለቶች በሙቀት እና በሚመራ ግፊት የሚፈጠሩ የተነባበረ ወይም የታሸገ መልክ አላቸው። እንደ ሆርንፍልስ፣ እብነ በረድ፣ ኳርትዚት እና ኖቫኩላይት ያሉ ፎላይድ ያልሆኑ ሜታሞርፊክ አለቶች የተደራረበ ወይም የታሸገ መልክ የላቸውም።
በ R ፕሮግራሚንግ ውስጥ መስመራዊ ሪግሬሽን ምንድን ነው?

መስመራዊ ሪግሬሽን በአንድ ወይም በብዙ የግብአት ትንበያ ተለዋዋጮች X ላይ በመመስረት ቀጣይነት ያለው ተለዋዋጭ Y ዋጋን ለመተንበይ ይጠቅማል። ዓላማው በምላሽ ተለዋዋጭ (Y) እና በተነበዩ ተለዋዋጮች (Xs) መካከል የሂሳብ ቀመር መፍጠር ነው። የ X እሴቶች ብቻ በሚታወቁበት ጊዜ Yን ለመተንበይ ይህንን ቀመር መጠቀም ይችላሉ።
የኒውተንን ሶስተኛ ህግ በስበት ኃይል ላይ ተግባራዊ ማድረግ እንችላለን?
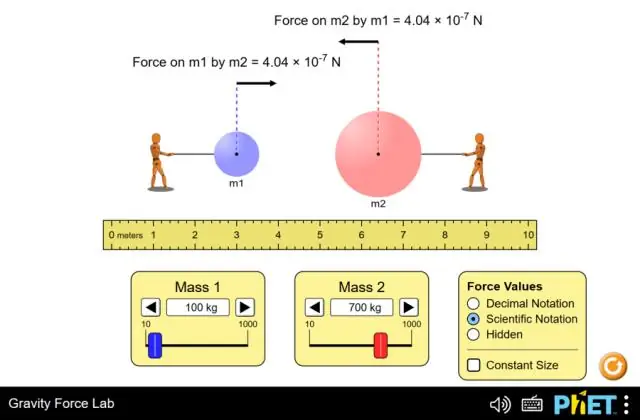
አዎ፣ የኒውተን ሶስተኛው ህግ ለስበት ኃይል ተፈጻሚ ነው። ስለዚህ ይህ ማለት ምድራችን በአንድ ነገር ላይ የመሳብ ሃይል ስታደርግ ነገሩ ደግሞ በተቃራኒው አቅጣጫ በምድር ላይ እኩል ሃይል ይሰራል ማለት ነው። ስለዚህ የኒውተንን ሶስተኛ ህግ በስበት ኃይል ላይ ተግባራዊ ማድረግ ትችላለህ ማለት እንችላለን
የሁለት መስመራዊ እኩልታዎች ስርዓት ምንም መፍትሄ እንዳይኖረው ማድረግ ይቻል ይሆን?

የመስመራዊ እኩልታዎች ስርዓቶች 0፣ 1 ወይም ማለቂያ የሌላቸው መፍትሄዎች ብቻ ሊኖራቸው ይችላል። እነዚህ ሁለት መስመሮች ሁለት ጊዜ መገናኘት አይችሉም. ትክክለኛው መልስ ስርዓቱ አንድ መፍትሄ አለው. ጠቅላላ የነጥብ ብዛት ባለ 2-ነጥብ ቅርጫት ብዛት ባለ 3-ነጥብ ቅርጫት 17 4 (8 ነጥብ) 3 (9 ነጥብ) 17 1 (2 ነጥብ) 5 (15 ነጥብ)
ቁርኝት መቼ መጠቀም እንዳለቦት እና መቼ ቀላል መስመራዊ ሪግሬሽን መጠቀም አለብዎት?

ሪግሬሽን በዋነኝነት የሚጠቀመው ሞዴሎችን/እኩልታዎችን ለመገንባት ቁልፍ ምላሹን ለመተንበይ ነው፣ Y፣ ከተነበዩ (X) ተለዋዋጮች ስብስብ። ቁርኝት በዋነኛነት በ2 ወይም ከዚያ በላይ በሆኑ የቁጥር ተለዋዋጮች መካከል ያለውን የግንኙነት አቅጣጫ እና ጥንካሬ በፍጥነት እና በአጭሩ ለማጠቃለል ይጠቅማል።
