ዝርዝር ሁኔታ:
ቪዲዮ: በግራፍ ላይ ነጥቦችን እንዴት መተርጎም ይቻላል?

2024 ደራሲ ደራሲ: Miles Stephen | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-15 23:33
ተብሎ ቢጠየቅ መተርጎም ሀ ነጥብ (x+1፣ y+1)፣ ወደ ትክክለኛው አንድ አሃድ ያንቀሳቅሱታል ምክንያቱም + በ x-ዘንግ ላይ ወደ ቀኝ ይሄዳል እና አንድ አሃድ ወደ ላይ ያንቀሳቅሱት ፣ ምክንያቱም + በy-ዘንጉ ላይ ወደ ላይ ይወጣል።
ከዚህ በተጨማሪ የትርጉም ቀመር ምንድን ነው?
በመጋጠሚያው አውሮፕላን ውስጥ መሳል እንችላለን ትርጉም አቅጣጫውን እና ስዕሉ ምን ያህል ርቀት መንቀሳቀስ እንዳለበት ካወቅን. ለ መተርጎም ነጥቡ P(x፣ y)፣ የቀኝ አሃዶች እና b አሃዶች፣ P'(x+a፣y+b) ይጠቀሙ።
በተጨማሪም ፣ ለውጦች እንዴት ይሰራሉ? ተግባር ለውጥ ማንኛውንም መሠረታዊ ተግባር ይወስዳል f (x) እና ከዚያ "ይለውጠዋል" (ወይም "መተርጎም") ይህም ቀመሩን ትንሽ ቀይረህ ግራፉን አንቀሳቅስ የሚለው አሪፍ መንገድ ነው። ተግባሩን ወደ ታች ማንቀሳቀስ ይሰራል በተመሳሳይ መንገድ; f (x) - b f (x) ወደ ታች b ክፍሎች ተንቀሳቅሷል።
በዚህ መሠረት የምስል ነጥብ ምንድን ነው?
ነጸብራቅ - የ ነጥብ የተሰጠው ነጥብ P በመስተዋቱ ውስጥ "የተንጸባረቀ" እና በመስመሩ በሌላኛው በኩል እኩል ርቀት ይታያል. ነጸብራቅ የ ነጥብ ከመስመሩ በላይ የሆነው P' ("P prime" ይባላል) በተባለው ስምምነት ነው እና "" ይባላል ምስል " የ ነጥብ ፒ.
ተግባርን እንዴት መቀየር ይቻላል?
የተግባር ትርጉም/የመቀየር ህጎች፡-
- f (x) + b ተግባሩን ለ ክፍሎችን ወደ ላይ ይለውጣል።
- f (x) - b ተግባሩን b ክፍሎችን ወደ ታች ይቀየራል።
- f (x + b) ተግባር b ክፍሎችን ወደ ግራ ይቀይራል።
- ረ (x - ለ) ተግባሩን b ክፍሎችን ወደ ቀኝ ይቀየራል።
- -f (x) በ x-ዘንጉ ውስጥ ያለውን ተግባር ያንፀባርቃል (ይህም ተገልብጦ ወደ ታች)።
የሚመከር:
ስዕልን በሂሳብ እንዴት መተርጎም ይቻላል?
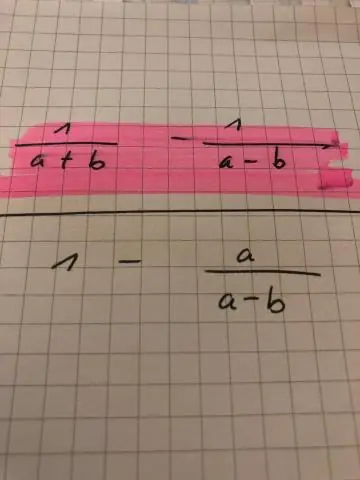
ቪዲዮ በዚህ ረገድ ምስልን በሂሳብ እንዴት መተርጎም ይቻላል? በ ትርጉም , የእቃው እያንዳንዱ ነጥብ በአንድ አቅጣጫ እና በተመሳሳይ ርቀት መንቀሳቀስ አለበት. አንድ በማከናወን ላይ ሳለ ትርጉም የመጀመሪያው ነገር ቅድመ- ምስል , እና እቃው ከ በኋላ ትርጉም ተብሎ ይጠራል ምስል . የትርጉም ቀመር ምንድን ነው? በመጋጠሚያው አውሮፕላን ውስጥ መሳል እንችላለን ትርጉም አቅጣጫውን እና ስዕሉ ምን ያህል ርቀት መንቀሳቀስ እንዳለበት ካወቅን.
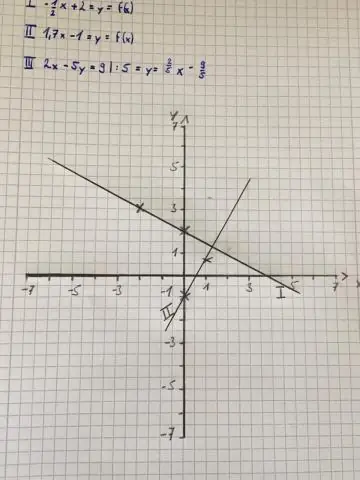
በግራፍ ውስጥ ያለውን ቋሚ ተመጣጣኝነት እንዴት ማግኘት ይቻላል?
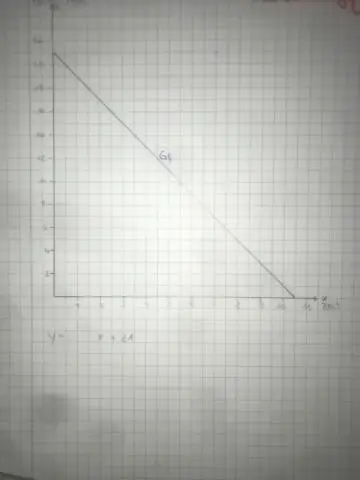
የእርስዎን ቋሚ የተመጣጣኝነት ከግራፍ ለማግኘት እነዚህን ደረጃዎች ይከተሉ፡ ሁለት ቀላል ነጥቦችን ያግኙ። በግራኛው ነጥብ ይጀምሩ እና ወደ ሁለተኛው ነጥብዎ ለመድረስ ስንት ካሬዎች እንደሚያስፈልግዎ ይቁጠሩ። ወደ ቀኝ ለመሄድ ስንት ካሬዎች እንደሚያስፈልግዎ ይቁጠሩ. ቀለል ያድርጉት፣ እና የእርስዎን ቋሚ ተመጣጣኝነት አግኝተዋል
የሁለት ነጥቦችን አካል ቅርፅ እንዴት ማግኘት ይቻላል?

አንድ የመነሻ ነጥብ የሚወክል እና ሌላኛው ደግሞ ተርሚናል ነጥብ የሚወክል ጋር ሁለት ነጥብ ቬክተር ተሰጥቷል. በሁለቱ ነጥብ ቬክተሮች የተሰራው የቬክተር አካል ቅርፅ በተርሚናል ነጥቡ አካላት ሲቀነስ የመነሻ ነጥብ ተጓዳኝ አካላት ይሰጣል
የወላጅ ተግባርን እንዴት መተርጎም ይቻላል?
ቪዲዮ ከእሱ፣ ተግባርን እንዴት መተርጎም ይቻላል? አንድን ተግባር በአግድም ለመተርጎም፣ በተግባሩ ውስጥ 'x-h'ን በ 'x' ይተኩ። የ'h' እሴት ግራፉ ምን ያህል ወደ ግራ ወይም ቀኝ እንደሚቀየር ይቆጣጠራል። በእኛ ምሳሌ, ከ h = -4 ጀምሮ, ግራፉ 4 ክፍሎችን ወደ ግራ ይቀየራል. አንድን ተግባር በአቀባዊ ለመተርጎም 'k'ን ወደ መጨረሻው ያክሉ። እንዲሁም አንድ ተግባር እንዴት ወደ ላይ እንደሚያንቀሳቅሱ ሊጠይቅ ይችላል?
በግራፍ ላይ በሁለት ነጥቦች መካከል ያለውን ርቀት እንዴት ማግኘት ይቻላል?
እርምጃዎች በመካከላቸው ያለውን ርቀት ለማወቅ የሚፈልጉትን የሁለት ነጥቦች መጋጠሚያዎች ይውሰዱ። አንድ ነጥብ 1(x1፣y1) ይደውሉ እና ሌላውን ነጥብ 2 (x2፣y2) ያድርጉ። የርቀት ቀመርን እወቅ። በነጥቦቹ መካከል ያለውን አግድም እና አቀባዊ ርቀት ያግኙ። ሁለቱንም እሴቶች ካሬ. አራት ማዕዘን እሴቶችን አንድ ላይ ይጨምሩ። የእኩልታውን ካሬ ሥር ውሰድ
