
ቪዲዮ: የሃሳብ ካርታዎች ጠቃሚ ናቸው?

2024 ደራሲ ደራሲ: Miles Stephen | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-15 23:33
የፅንሰ-ሀሳብ ካርታዎች በተለይ ናቸው። ጠቃሚ በማየት የተሻለ ለሚማሩ ተማሪዎች፣ ምንም እንኳን የትኛውንም አይነት ተማሪ ሊጠቅሙ ይችላሉ። እነሱ ኃይለኛ የጥናት ስልት ናቸው ምክንያቱም ትልቁን ምስል እንዲያዩ ስለሚረዱ - ምክንያቱም በከፍተኛ ደረጃ ስለሚጀምሩ ጽንሰ-ሐሳቦች ትርጉም ባለው ግንኙነት ላይ በመመስረት መረጃን ለመቁረጥ ይረዳሉ።
ከዚያም ካርታዎች አንባቢን እንዴት ይረዳሉ?
ጽንሰ-ሐሳብ ካርታዎች ይችላል መርዳት ስለምትጠኚው ርዕስ ያለዎትን ግንዛቤ ያሻሽላሉ። ጽንሰ-ሀሳብ መፍጠር ካርታዎች ይረዳል በምታጠኑዋቸው ሃሳቦች መካከል ያለውን ግንኙነት አጠናክር። ጽንሰ-ሐሳብ ሲፈጥሩ ካርታ የጽሑፍ ምንባብ ስታነብ ወይም በኋላ፣ በአንቀጹ ውስጥ ባሉት ሃሳቦች መካከል ያለውን ግንኙነት ታሰላስላለህ።
የፅንሰ-ሀሳብ ካርታ ፊዚካል ሳይንስን በማስተማር ጠቃሚ ነው? ይህ ጥናት እንደሚጠቁመው የፅንሰ-ሀሳብ ካርታ እንደ ሀ ጠቃሚ መሳሪያ በ ሳይንስ ተማሪዎች እንዲገነዘቡ በመርዳት ትምህርት ጽንሰ-ሐሳቦች በቀላሉ፣ ቅድመ ግንዛቤን ከአዲስ እውቀት ጋር ያገናኙ እና ስለእነዚያ ያላቸውን ግንዛቤ ይወክላሉ ጽንሰ-ሐሳቦች.
በዚህ መሠረት ስለ ጽንሰ-ሐሳብ ካርታ በጣም አስፈላጊው ነገር ምንድን ነው?
የፅንሰ-ሀሳብ ካርታዎች የተዋበ፣ በቀላሉ ሊረዳ የሚችል የባለሙያ ጎራ እውቀት ውክልና ያቅርቡ። ናቸው ተጨማሪ እንደ ድሮች፣ በመካከላቸው ያሉ አገናኞችን ያሳያል ጽንሰ-ሐሳቦች በ ሀ ተጨማሪ ውስብስብ መንገድ, እና በጣም ከቀላል እስከ በጣም ውስብስብ ለሆኑ ውስብስብ ነገሮች መፍቀድ ይችላሉ.
የፅንሰ-ሀሳብ ካርታ ዘዴ ምንድነው?
የፅንሰ-ሀሳብ ካርታ . የማህበራዊ ሳይንቲስቶች በርካታ አዘጋጅተዋል ዘዴዎች እና የምርምር ፕሮጀክት ለመቅረጽ እርስዎን ለመርዳት ጠቃሚ ሊሆኑ የሚችሉ ሂደቶች። የፅንሰ-ሀሳብ ካርታ አጠቃላይ ነው። ዘዴ ማንኛውም ግለሰብ ወይም ቡድን ስለ አንዳንድ ርዕሰ ጉዳዮች በምስል መልክ ሀሳባቸውን እንዲገልጹ ለመርዳት ጥቅም ላይ ሊውል ይችላል.
የሚመከር:
ጭብጥ ካርታዎች እንዴት ጠቃሚ ናቸው?
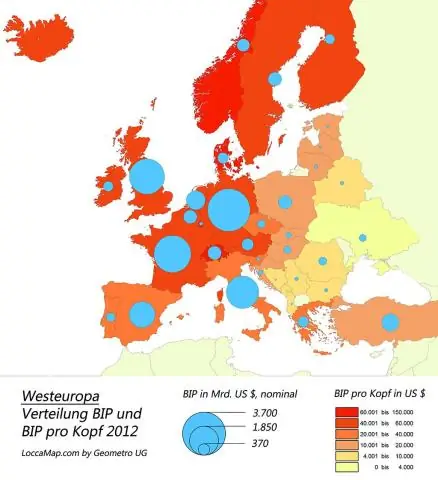
ካርታዎች የካርታ አንባቢዎች በካርታው ላይ ካለው ጂኦግራፊያዊ አካባቢ ጋር እንዲተዋወቁ ለማገዝ እንደ የቦታ ስሞች ወይም ዋና ዋና የውሃ አካላት ያሉ አንዳንድ የአካባቢ ወይም የማጣቀሻ መረጃዎችን በመደበኛነት ያካትታሉ። ሁሉም ቲማቲክ ካርታዎች በሁለት አስፈላጊ አካላት የተዋቀሩ ናቸው፡ የመሠረት ካርታ እና ስታቲስቲካዊ መረጃ
የኮምፒተር ሞዴሎች በሳይንስ ውስጥ ለምን ጠቃሚ ናቸው?

የገሃዱ ዓለም ክስተቶችን ውክልና ለመፍጠር ኮምፒውተሮች የሂሳብ፣ ዳታ እና የኮምፒውተር መመሪያዎችን ይጠቀማሉ። ውስብስብ በሆኑ ሁኔታዎች ውስጥ፣ ከአየር ንብረት ሥርዓት ጀምሮ በከተማው ውስጥ የሚናፈሰውን አሉባልታ እስከ መስፋፋት ድረስ ያለውን - ወይም ምን ሊሆን እንደሚችል ሊተነብዩ ይችላሉ።
መለኪያዎችን በሚዘግቡበት ጊዜ ጠቃሚ አሃዞች ለምን አስፈላጊ ናቸው?

የመልሱን ትክክለኛነት ለማሳየት ጉልህ የሆኑ አሃዞች አስፈላጊ ናቸው። ይህ በሳይንስ እና ምህንድስና አስፈላጊ ነው ምክንያቱም የትኛውም የመለኪያ መሣሪያ መቶ በመቶ ትክክለኛነትን ሊለካ አይችልም። ጉልህ የሆኑ አሃዞችን መጠቀም ሳይንቲስቱ መልሱ ምን ያህል ትክክል እንደሆነ ወይም ምን ያህል እርግጠኛ አለመሆን እንዳለ እንዲያውቅ ያስችለዋል።
የጂኖሚክ ቤተ-መጻሕፍት ለምን ጠቃሚ ናቸው?

ሁሉም የዲ ኤን ኤ ቤተ-መጻሕፍት አንድ የተወሰነ ባዮሎጂያዊ የፍላጎት ሥርዓትን የሚወክሉ የዲ ኤን ኤ ቁርጥራጮች ስብስቦች ናቸው። ተመራማሪዎች ዲኤንኤውን ከአንድ አካል ወይም ቲሹ በመተንተን ለተለያዩ ጠቃሚ ጥያቄዎች መልስ መስጠት ይችላሉ። ለእነዚህ የዲኤንኤ ስብስቦች ሁለቱ በጣም የተለመዱ አጠቃቀሞች የዲኤንኤ ቅደም ተከተል እና የጂን ክሎኒንግ ናቸው።
ለምን የኢንፍራሬድ ቴሌስኮፖች ጠቃሚ ናቸው?

የኢንፍራሬድ አስትሮኖሚ ሳይንቲስቶች የፕላኔቶችን፣ የከዋክብትን እና የአቧራውን የሙቀት መጠን በፕላኔቶች መካከል ያለውን የሙቀት መጠን የመለካት ችሎታ ይሰጣቸዋል። የኢንፍራሬድ ጨረሮችን አጥብቀው የሚወስዱ ብዙ ሞለኪውሎችም አሉ። ስለዚህ የአስትሮፊዚካል አካላት ስብጥር ጥናት ብዙውን ጊዜ በተሻለ ኢንፍራሬድ ቴሌስኮፖች ይከናወናል
