ዝርዝር ሁኔታ:

ቪዲዮ: ሁለት ነጥቦችን ከተሰጠው በነጥብ ቁልቁል ቅጽ እንዴት ይፃፉ?

2024 ደራሲ ደራሲ: Miles Stephen | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-15 23:33
የተለያዩ ናቸው። ቅጾች የምንችለውን ጻፍ የ እኩልታ የአንድ መስመር፡ የ ነጥብ - ተዳፋት ቅጽ ፣ የ ተዳፋት - መጥለፍ ቅጽ ፣ ደረጃው ቅጽ ወዘተ እኩልታ የአንድ መስመር ሁለት ነጥብ ተሰጥቷል (x1፣ y1) እና (x2፣ y2) መስመሩ የሚያልፍበት ነው። ተሰጥቷል በ፣ ((y - y1)/(x - x1)) / ((y2 - y1)/(x2 - x1))።
በተጨማሪም ፣ ሁለት ነጥብ የተሰጠውን የመስመር እኩልታ እንዴት ይፃፉ?
ያግኙ የተሰጠው መስመር እኩልታ እርስዎ የሚያውቁት ሁለት ነጥቦች ያልፋል። የ የአንድ መስመር እኩልታ በተለምዶ y=mx+b ተብሎ የተጻፈ ሲሆን m ዳገቱ ሲሆን b ደግሞ y-intercept ነው።
ከዚህ በላይ፣ የነጥብ ቁልቁለት ቅፅ ፍቺ ምንድነው? የነጥብ ፍቺ - ተዳፋት ቅጽ . በ ውስጥ ቀጥተኛ መስመር እኩልታ ቅጽ y - y1 = ሜትር (x - x1) m የት ነው ተዳፋት የመስመሩ እና (x1, y1) የተሰጠ መጋጠሚያዎች ናቸው። ነጥብ በመስመር ላይ - ማወዳደር ተዳፋት - መጥለፍ ቅጽ.
ይህንን ከግምት ውስጥ በማስገባት ሁለት ነጥብ የተሰጠውን ቁልቁል እንዴት ማግኘት ይቻላል?
የቀጥታ መስመር ተዳፋትን ለማስላት ሶስት እርከኖች አሉ።
- ደረጃ አንድ፡ በመስመሩ ላይ ሁለት ነጥቦችን ለይ።
- ደረጃ ሁለት፡ አንዱን ለመሆን (x1፣ y1) እና ሌላውን (x2፣ y2) ምረጥ።
- ደረጃ ሶስት፡ ተዳፋትን ለማስላት የዳገቱን እኩልታ ይጠቀሙ።
Y መጥለፍ ቅጽ ምንድን ነው?
በቀጥተኛ መስመር እኩልታ (እኩልታው እንደ "ሲፃፍ) y = mx + b")፣ ቁልቁል በ x ላይ የሚባዛው “m” ቁጥር ሲሆን “b” ደግሞ y - መጥለፍ (ይህም መስመሩ ቀጥ ብሎ የሚያልፍበት ነጥብ ነው። y - ዘንግ). ይህ ጠቃሚ ቅጽ የመስመሩ እኩልታ በማስተዋል “slope- የመጥለፍ ቅጽ ".
የሚመከር:
ነጥቦችን በሚዛን እንዴት ይመዝናሉ?

እንግዲህ አንድ ነጥብ የአንድ ግራም አሥረኛ ነው። መጀመሪያ 1ጂ ሚዛን ትፈልጋለህ ስለዚህ ከምትመዝነው ቀጥሎ 1ጂ ክብደት ተጠቀም። ከፍ ያለ ወይም ዝቅተኛ ነጥብ አለህ፣ ስለዚህ 1.1 እስኪያነብ ድረስ ብትጨምር ዝቅተኛ ነጥብ ነው። 1.2 እስኪያነብ ድረስ ካከሉ 1.1 እስኪያነብ ድረስ የተወሰነውን ያስወግዱ - ከፍተኛ ነጥብ ነው።
የሁለት ነጥቦችን አካል ቅርፅ እንዴት ማግኘት ይቻላል?

አንድ የመነሻ ነጥብ የሚወክል እና ሌላኛው ደግሞ ተርሚናል ነጥብ የሚወክል ጋር ሁለት ነጥብ ቬክተር ተሰጥቷል. በሁለቱ ነጥብ ቬክተሮች የተሰራው የቬክተር አካል ቅርፅ በተርሚናል ነጥቡ አካላት ሲቀነስ የመነሻ ነጥብ ተጓዳኝ አካላት ይሰጣል
በግራፍ ላይ ነጥቦችን እንዴት መተርጎም ይቻላል?
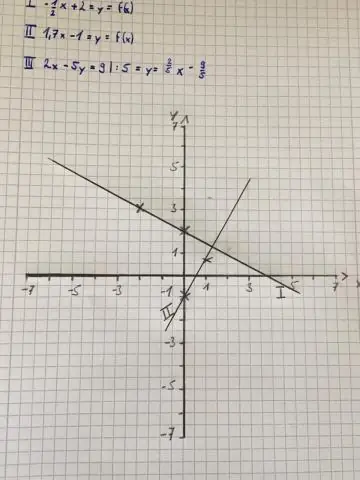
አንድን ነጥብ (x+1፣y+1) እንዲተረጎም ከተጠየቅህ ወደ ቀኝ አንድ አሃድ ያንቀሳቅሱታል ምክንያቱም + በ x-ዘንግ ላይ ወደ ቀኝ ይሄዳል እና አንድ አሃድ ወደ ላይ ያንቀሳቅሱት ምክንያቱም + በy-ዘንግ ላይ ወደ ላይ ይወጣል
Biconditional እንደ ሁለት ቅድመ ሁኔታዎች እንዴት ይፃፉ?
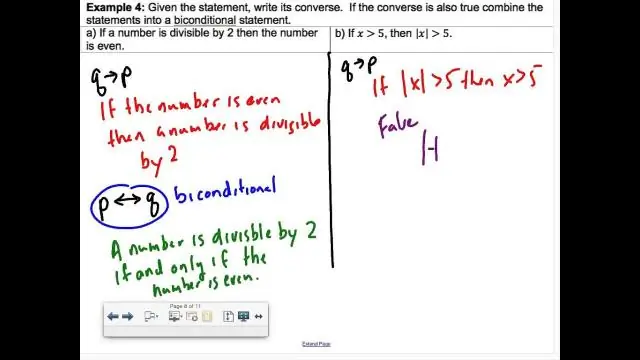
የሁለት ሁኔታዊ መግለጫዎች ጥምረት ነው, "ሁለት መስመር ክፍሎች ከተጣመሩ እኩል ርዝመት አላቸው" እና "ሁለት መስመር ክፍሎች እኩል ርዝመት ካላቸው ከዚያም እነሱ የተጣመሩ ናቸው". ሁለቱ ቅድመ ሁኔታዎች እውነት ከሆኑ እና ብቻ ከሆነ ባለ ሁለት ሁኔታ እውነት ነው። Bi-ሁኔታዎች ምልክት ይወከላሉ ↔ ወይም ⇔
በጂኦሜትሪ ውስጥ ነጥቦችን እንዴት ይለያሉ?

ነጥብ በጣም መሠረታዊው የቁስ ኢንጂኦሜትሪ ነው። እሱ በነጥብ ይወከላል እና በካፒታል ፊደል ይሰየማል። አንድ ነጥብ ቦታን ብቻ ይወክላል; ዜሮ መጠን አለው (ይህም ዜሮ ርዝመት፣ ዜሮ ስፋት እና ዜሮ ቁመት) ነው። ምስል 1 ነጥብ Cን፣ ነጥብ M እና ነጥብ Qን ያሳያል
