
ቪዲዮ: የአንድ መስመር እኩልታ ከተጠቀሰው መስመር ጋር ትይዩ እና በተሰጠው መስመር ላይ ባለ ነጥብ ማግኘት ምክንያታዊ ይሆናል?

2024 ደራሲ ደራሲ: Miles Stephen | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-15 23:33
የ የአንድ መስመር እኩልታ የሚለውን ነው። ትይዩ ነው። ወይም በተሰጠው መስመር ላይ ቀጥ ያለ ? ሊሆን የሚችል መልስ: የ ተዳፋት ትይዩ መስመሮች እኩል ናቸው. የሚታወቀውን ተዳፋት እና መጋጠሚያዎች ሀ ነጥብ በሌላ መስመር ወደ ውስጥ ነጥብ - ተዳፋት ቅጽ ወደ እኩልታውን ያግኙ የእርሱ ትይዩ መስመር.
በዚህ ረገድ፣ ከተሰጠው መስመር ጋር ትይዩ የሆነ ቀመር እንዴት ይፃፉ?
ሁለት መስመሮች ናቸው። ትይዩ ተመሳሳይ ቁልቁል ካላቸው. ለምሳሌ 1: የ ተዳፋት ያግኙ መስመር ትይዩ ወደ መስመር 4x - 5y = 12. የዚህን ቁልቁል ለማግኘት መስመር ማግኘት አለብን መስመር ወደ slope-intercept form (y = mx + b)፣ ይህም ማለት ለ y: የቁልቁለት ቁልቁል መፍታት አለብን ማለት ነው። መስመር 4x - 5y = 12 m = 4/5 ነው.
የቋሚ መስመር እኩልታ ምንድነው? የተሰጠው እኩልታ ደረጃውን የጠበቀ ነው፣ስለዚህ ወደ slope-intercept form መቀየር አለበት፡ y = mx + b ቁልቁለቱን ለማወቅ -2/3 ነው። መ ሆ ን ቀጥ ያለ አዲሱ ቁልቁል 3/2 መሆን አለበት (ከአሮጌው ተዳፋት ተቃራኒ)።
በሁለተኛ ደረጃ, በመነሻው ውስጥ የሚያልፍ እና ትይዩ የሆነው የመስመሩ እኩልታ ምንድን ነው?
የመስመሩ መደበኛ ቅርፅ y=mx +b ነው። የምንፈልገው መስመር ከላይ ካለው ጋር ትይዩ ስለሆነ ገደላማዎቹ ተመሳሳይ መሆናቸውን ይነግረናል። የምንፈልገው እኩልታ መስመር ነጥብን (0፣ 0) በሚሰጠው መነሻ በኩል ያልፋል እና እኛ እናውቃለን ተዳፋት m= 2/17.
እነዚህ መስመሮች ቀጥ ያሉ ናቸው?
ማብራሪያ፡- ሁለት መስመሮች ናቸው። ቀጥ ያለ ከሆነ እና የእነሱ ተዳፋት አሉታዊ ተገላቢጦሽ ከሆነ. ማግኘት የ ተዳፋት, ማስቀመጥ አለብን የ እኩልነት ወደ ተዳፋት-መጠለፍ ቅጽ,, የት እኩል የ ተዳፋት የ መስመሩ . ስለዚህ, ማንኛውም መስመር በቋሚ ተዳፋት መሆን አለበት.
የሚመከር:
የአንድ መስመር አካል ምንድን ነው እና አንድ የመጨረሻ ነጥብ አለው?

ሬይ፡ አንድ የመጨረሻ ነጥብ ያለው እና በአንድ አቅጣጫ ያለ መጨረሻ የሚቀጥል የመስመር አካል ነው።
አንድ ነጥብ እና ትይዩ መስመር የተሰጠውን መስመር እኩልታ እንዴት ማግኘት ይቻላል?

በተዳፋት-መጠለፍ ቅጽ ውስጥ ያለው የመስመሩ እኩልታ y=2x+5 ነው። የትይዩው ቁልቁል ተመሳሳይ ነው: m=2. ስለዚህ፣ የትይዩ መስመር እኩልታ y=2x+a ነው። ሀ ለማግኘት፣ መስመሩ በተሰጠው ነጥብ ውስጥ ማለፍ አለበት የሚለውን እውነታ እንጠቀማለን፡5=(2)⋅(−3)+a
የአንድ መስመር ክፍል ቋሚ ባለ ሁለት ክፍል እኩልታ እንዴት ማግኘት ይቻላል?

በነጥብ-ቁልቁል ቅጽ፣ y - k =m(x - h) ላይ እኩልታ ይፃፉ፣ የ perpendicular bisector anda point (h፣ k) bisector የሚያልፍበት ቁልቁል ስለሚታወቅ። y = mx + b ለማግኘት የነጥብ-ቁልቁለት እኩልታ ይፍቱ። የተንሸራታች እሴት ያሰራጩ። የ k እሴቱን ወደ እኩልታው በቀኝ በኩል ይውሰዱት።
የአንድ መስመር እኩልታ ከ Y ዘንግ ጋር ምን ያህል ነው?

ማብራሪያ፡ በ y ዘንግ ላይ ቀጥ ያለ መስመር አግድም መስመር ይሆናል፣ የማንኛውም አግድም መስመር እኩልታ y=b ሲሆን ለ y-መጠለፍ ነው።
የአንድ ነጥብ የዋልታ መጋጠሚያዎችን እንዴት ማግኘት ይቻላል?
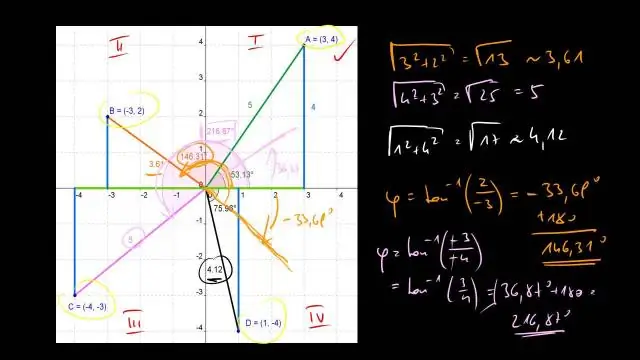
ከካርቴዥያን መጋጠሚያዎች (x,y) ወደ ዋልታ መጋጠሚያዎች (r,θ): r = √ (x2 + y2) θ = tan-1 (y / x) ለመለወጥ
