የመስመር ተግባራትን እንዴት ይለውጣሉ?

ዝርዝር ሁኔታ:

የተግባር ትርጉም/የመቀየር ህጎች፡-

ቪዲዮ: የመስመር ተግባራትን እንዴት ይለውጣሉ?

2024 ደራሲ ደራሲ: Miles Stephen | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-15 23:33

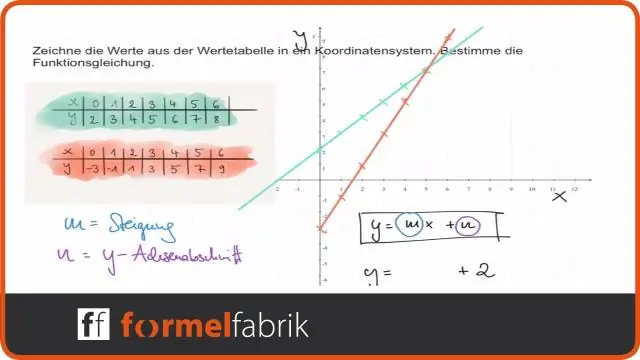
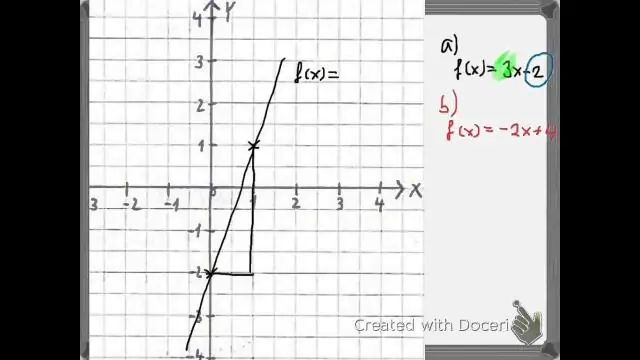
እንዴት ማድረግ እንደሚቻል፡- ከሀ እኩልነት ከተሰጠ መስመራዊ ተግባር ፣ ተጠቀም ለውጦች ግራፍ ለማድረግ መስመራዊ ተግባር በቅጹ f(x)=mx+b f (x) = m x + b. ግራፍ f(x)=x f (x) = x. ግራፉን በአቀባዊ ዘርጋ ወይም ጨመቀው በፋክታር |m|። ግራፉን ወደ ላይ ወይም ወደ ታች ያዙሩት b አሃዶች።

እንደዚያው፣ የመስመራዊ ተግባርን ለውጥ እንዴት ይገልጹታል?

ግራፍ የ መስመራዊ ተግባር (አንድ መስመር) በመጋጠሚያው ፍርግርግ ዙሪያ ሊንቀሳቀስ ይችላል. ይህ ይባላል ሀ ለውጥ . ሶስት መሰረታዊ ነገሮች አሉ። ለውጦች : መተርጎም (መስመሩን ዙሪያውን ማንሸራተት)፣ ነጸብራቅ (መስመሩን መገልበጥ) እና ማዛባት (መስመሩን መዘርጋት)። መንቀሳቀስ ይችላሉ ( መለወጥ ) መስመሩ በአቀባዊ ወይም በአግድም.

እንዲሁም፣ የትኞቹ ለውጦች የመስመራዊ ተግባርን ቁልቁል ላይ ተጽዕኖ ያሳድራሉ? መለወጥ መስመራዊ ተግባራት (መለጠጥ እና መጭመቅ) መዘርጋት እና መጨናነቅ ይለውጣሉ የመስመር ተግባር ተዳፋት . መስመሩ ሾጣጣ ከሆነ, እ.ኤ.አ ተግባር በአቀባዊ ተዘርግቷል ወይም በአግድም ተጨምቋል።

በዚህ መሠረት አንድን ተግባር እንዴት ይለውጣሉ?

የተግባር ትርጉም/የመቀየር ህጎች፡-

f (x) + b ተግባሩን ለ ክፍሎችን ወደ ላይ ይለውጣል።
f (x) - b ተግባሩን b ክፍሎችን ወደ ታች ይቀየራል።
f (x + b) ተግባር b ክፍሎችን ወደ ግራ ይቀይራል።
ረ (x - ለ) ተግባሩን b ክፍሎችን ወደ ቀኝ ይቀየራል።
-f (x) በ x-ዘንጉ ውስጥ ያለውን ተግባር ያንፀባርቃል (ይህም ተገልብጦ ወደ ታች)።

ተግባርን እንዴት ያንፀባርቃሉ?

ሀ ተግባር መሆን ይቻላል ተንጸባርቋል ስለ ዘንግ በአሉታዊ በማባዛት. ለ ማንጸባረቅ ስለ y-ዘንግ፣ -x ለማግኘት እያንዳንዱን x በ -1 ማባዛት። ለ ማንጸባረቅ ስለ x-ዘንግ፣ -f(x) ለማግኘት f(x) በ -1 ማባዛት።

የሚመከር:

የተዋሃዱ ተግባራትን እንዴት ይገመግማሉ?

ግራፎችን በመጠቀም የተዋሃዱ ተግባራትን መገምገም የተሰጠውን ግቤት በግራፉ x-ዘንግ ላይ ወደ ውስጠኛው ተግባር ይፈልጉ። የውስጣዊውን ተግባር ውፅዓት ከግራፉ y-ዘንግ አንብብ። በውጪው ተግባር ግራፍ ላይ ባለው የ x- ዘንግ ላይ የውስጣዊ ተግባር ውጤቱን ያግኙ

የተዋሃዱ ተግባራትን እንዴት ማባዛት ይቻላል?

የተግባሮች ማባዛት እና ቅንብር አንድን ተግባር በስካላር ለማባዛት፣ እያንዳንዱን ውጤት በዚያ scalar ያባዙ። f (g(x)ን) ስንወስድ g(x) እንደ የተግባሩ ግብአት እንወስዳለን። ለምሳሌ f (x) = 10x እና g(x) = x + 1፣ ከዚያም f (g(4)) ለማግኘት፣ g(4) = 4 + 1 + 5ን እናገኛለን፣ እና f (5)ን እንገመግማለን። ) = 10(5) = 50. ምሳሌ፡ f (x) = 2x - 2, g(x) = x2 - 8