
ቪዲዮ: የኳድራቲክ ተግባር ምሳሌያዊ ውክልና እንዴት ማግኘት ይቻላል?

2024 ደራሲ ደራሲ: Miles Stephen | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-15 23:33
ባለአራት ተግባራት በምሳሌያዊ ሁኔታ ሊወከል ይችላል እኩልታ , y (x) = መጥረቢያ2 + bx + c፣ ሀ፣ b እና c ቋሚዎች ሲሆኑ፣ እና ≠ 0. ይህ ቅጽ እንደ መደበኛ ቅፅ ተጠቅሷል።
ሰዎች ደግሞ የአንድ ተግባር ምሳሌያዊ ውክልና ምንድነው?
ተግባራት . ምናልባት እርስዎ በደንብ ያውቃሉ ምሳሌያዊ ውክልና የ ተግባራት , እንደ ቀመር, y = f (x). ተግባራት በጠረጴዛዎች ሊወከል ይችላል ፣ ምልክቶች , ወይም ግራፎች.
በተመሳሳይ የኳድራቲክ ግራፍ ቅርፅን እንዴት እንደሚወስኑ? የፓራቦላ ቅርጽ
- ከ a> 0፣ እንግዲያውስ ፓራቦላ ዝቅተኛ ነጥብ አለው እና ወደ ላይ ይከፈታል (U-shaped) ለምሳሌ።
- a<0 ከሆነ፣ ፓራቦላ ከፍተኛው ነጥብ አለው እና ወደ ታች ይከፈታል (n-ቅርጽ ያለው) ለምሳሌ።
- (ሀ) U-ቅርጽ ያለው ወይም n-ቅርጽ ያለው መሆኑን ለመወሰን a>0 ወይም a<0 መሆኑን ያረጋግጡ።
- (ሐ) የy-intercept መጋጠሚያዎች (ምትክ x=0)።
በዚህ መሠረት አራት ተግባራትን እንዴት ይወክላሉ?
ግራፎች ሀ ኳድራቲክ ተግባር ከቅጹ አንዱ ነው f(x) = መጥረቢያ2 + bx + c፣ ሀ፣ b እና c ከዜሮ ጋር እኩል ያልሆኑ ቁጥሮች ሲሆኑ። ግራፍ የ ኳድራቲክ ተግባር ፓራቦላ የሚባል ኩርባ ነው። ፓራቦላዎች ወደ ላይ ወይም ወደ ታች ሊከፈቱ እና በ"ወርድ" ወይም "ቁልቁለት" ሊለያዩ ይችላሉ ነገር ግን ሁሉም ተመሳሳይ የ"U" ቅርፅ አላቸው።
ተግባርን እንዴት መፍታት ይቻላል?
ለ ተግባራት , ሁለቱ ምልክቶች አንድ አይነት ትርጉም አላቸው, ነገር ግን "f (x)" የበለጠ ተለዋዋጭነት እና ተጨማሪ መረጃ ይሰጥዎታል. "y = 2x + 3" ትል ነበር። መፍታት ለ y መቼ x = -1" አሁን "f (x) = 2x + 3; አግኝ f (–1)" ("f-of-x ከ2x ሲደመር ሶስት ጋር እኩል ነው፤ f-of-negative-oneን ፈልግ")።
የሚመከር:
ባዶ ፋክተር ህግን በመጠቀም የኳድራቲክ እኩልታን እንዴት መፍታት ይቻላል?

ከዚህ መረዳት የምንችለው፡ የሁለቱ ቁጥሮች ውጤት ዜሮ ከሆነ፡ አንድ ወይም ሁለቱም ቁጥሮች ዜሮ ናቸው። ማለትም ab = 0 ከሆነ, ከዚያም a = 0 ወይም b = 0 (ይህም a = b = 0 የሚለውን ያካትታል). ይህ የኑል ፋክተር ህግ ይባላል; እና ኳድራቲክ እኩልታዎችን ለመፍታት ብዙ ጊዜ እንጠቀማለን።
የኳድራቲክ ተግባር እኩልነት ምንድን ነው?
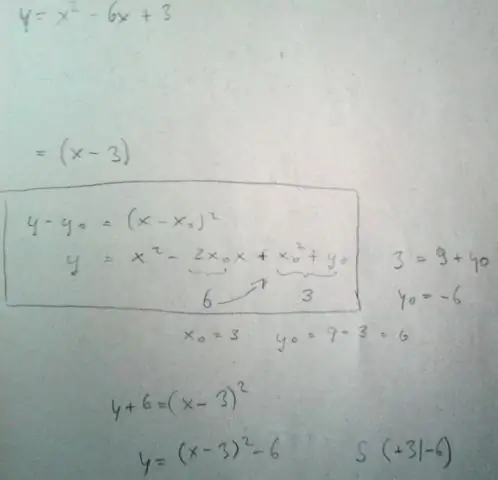
ኳድራቲክ ተግባር ከ f(x) = ax2 + bx + c አንዱ ሲሆን a፣ b እና c ከዜሮ ጋር እኩል ያልሆኑ ቁጥሮች ናቸው። የኳድራቲክ ተግባር ግራፍ ፓራቦላ የሚባል ኩርባ ነው። ፓራቦላዎች ወደ ላይ ወይም ወደ ታች ሊከፈቱ ይችላሉ እና በ'ወርድ' ወይም 'ገደል' ሊለያዩ ይችላሉ፣ ግን ሁሉም ተመሳሳይ የ'U' ቅርፅ አላቸው።
በኳድራቲክ ተግባር ውስጥ እንዴት ማግኘት ይቻላል?
ኳድራቲክ ተግባር f(x) = a(x -h)2 + k፣ ከዜሮ ጋር እኩል ያልሆነ፣ መደበኛ ቅርጽ አለው ተብሏል። a አዎንታዊ ከሆነ, ግራፉ ወደ ላይ ይከፈታል, እና አሉታዊ ከሆነ, ወደ ታች ይከፈታል. የሲሜትሪ መስመሩ ቁመታዊ መስመር x = h ነው፣ እና ወርድ ነጥቡ(h፣k) ነው።
የኳድራቲክ ተግባር ከፍተኛውን እሴት እንዴት ማግኘት ይቻላል?

ቀመር y = ax2 + bx + c ከተሰጠህ ቀመሩን max =c- (b2/4a) በመጠቀም ከፍተኛውን ዋጋ ማግኘት ትችላለህ። እኩልታ y = a(x-h)2 + k ካሎት እና ቲያትር ቤቱ አሉታዊ ከሆነ ከፍተኛው እሴት k ነው።
የአንድ ተግባር ምሳሌያዊ ውክልና ምንድን ነው?

ተግባራት እንደ ቀመር፣ y = f(x) ያሉ ተግባራትን ምሳሌያዊ ውክልና በደንብ ያውቁ ይሆናል። ተግባራት በሰንጠረዦች፣ ምልክቶች ወይም ግራፎች ሊወከሉ ይችላሉ።
